JAKOŚĆ   

Najbardziej korzystnym warunkiem do wdrożenia SPC jest produkcja ciągła lub w dużych seriach. Dla procesów cyklicznych jak np. wtryskiwanie, dobrze by zmiany formy na wtryskarce nie były częstsze niż co 2 tygodnie. Najlepszym parametrem do diagnozy procesu jest zwykle masa wypraski. Obecnie nie ma problemu z zakupem ( nieduży koszt ) i obsługą wag elektronicznych. Natomiast wybór parametru masy ma ograniczenia dla kształtek wtryskowych z zapraskami, gdy stosujemy surowiec o zmieniającej się  gęstości (np. gdy zmienia się zawartość włókna szklanego w kolejnych partiach stosowanego tworzywa sztucznego ) lub występują trudności w oddzielaniu wlewka przy jego zmiennej objętości ( ta zmieniająca się objętość dla wlewów normalnych też reprezentuje określoną stałość parametrów i może być miarą stabilności procesu ). Czyli nawet te ograniczenia, w pewnych warunkach, nie wykluczają stosowanie kart kontrolnych.

Swoje  doświadczenie opieram na zastosowaniu ręcznie prowadzonych kart kontrolnych na stanowiskach wtryskarek i przede wszystkim ten rodzaj przetwórstwa tworzyw sztucznych ono obejmuje, ale wiele niżej opisanych wniosków można rozszerzyć na inne technologie, nawet nie tylko ściśle tworzywowe. W stosowanych przez nas kartach kontrolnych istnieje możliwość rozszerzenia granic kontrolnych, w uzasadnionych przypadkach i ze świadomością pogorszenia nadzoru nad procesem. W samodzielnie opracowanym skoroszycie programu EXCEL można z łatwością te granice zmienić o każdą, odpowiednią, wielkość procentową w oparciu o nabyte doświadczenie.

Jednym z zaobserwowanych zjawisk okazała się czasami występująca zmiana objętości gniazda formy (zmiana masy wypraski) po rozebraniu i ponownym złożeniu formy. Zauważono też skutki uchylania połówek form  nie tylko przy dużych ciśnieniach w punkcie przełączania na docisk, ale także podczas wczesnych faz wypełniania formy. Jeżeli formy są mało sztywne zjawisko to będzie bardzo widoczne.

Zakresy linii kontrolnych obserwowanych zmian masy dla tworzyw bezpostaciowych są rzędu 0,5÷1,2%, zależeć mogą od sztywności formy, drogi płynięcia i konstrukcji wyrobu oraz w znaczącej najczęściej mierze, od siły zamknięcia formy.

Dla niemal każdego przetwórcy tworzyw sztucznych zastosowanie kart kontrolnych masy jest niezwykle łatwym sposobem sterowania rezultatami procesu wtryskiwania. Można jedynie wyznaczać linie kontrolne wynikłe z naturalnych granic procesu lub ustalać granice tolerancji masy ze względu na wady i uchybienia oraz określić zdolności procesu wytwarzania. Takie granice są dużo łatwiejsze do wyznaczenia i stosunkowo odporne na wpływ wszystkich niepożądanych współzależności.

Wracając do zdolności maszynowej, a więc parametrów tolerowanych, takich jak np. długość, aby określić C_mk, jak już wcześniej opisano, pobiera się próbkę kolejnych wtrysków (w naszym przypadku 50), po minimum 16 godzinach, w określonej temperaturze mierzy się wypraskę w przyrządzie zapewniającym dokładność i powtarzalność, a wynik otrzymuje się po wpisaniu danych pomiarowych i identyfikujących na arkusz Excel’a. Na towarzyszącym arkuszu naszego programu, można odczytać histogram rozkładu, wariancję, skośność i kurtozę (współczynnik skupienia).

Przy wszystkich pomiarach liniowych niezwykle ważna jest temperatura wypraski i wyeliminowanie wpływu tzw. „czynnika ludzkiego” na wymaganą dużą dokładność pomiaru. Przy bieżącej kontroli procesu wystarczy zwykle tylko odczytać temperaturę z dokładnego termometru, ale wymiar liniowy należy określać tylko w wyspecjalizowanym przyrządzie. Musi on zapewnić całkowitą niezależność do osoby mierzącego oraz ewentualnych innych czynników które mogłyby zniekształcić odczyt. Pomiary liniowe do określania C_mk należy wykonać w pomieszczeniu o stałej temperaturze (po minimum 2 godzinach kondycjonowania), najlepiej w 20°C.

Wpływ temperatury na wymiar liniowy jest rzędu 0,01%/K, natomiast zakres linii kontrolnych to rząd 0,05%. Można jeszcze dodać że skurcz wtórny dla tworzyw bezpostaciowych to rząd wartości 0,03%. Jeżeli rzeczywista temperatura wypraski będzie różniła się o 3K od przyjętej, to wykres ze środka zakresu wyjdzie poza linie kontrolne.

Zwykle przyjmuje się wartości współczynnika rozszerzalności termicznej tworzyw sztucznych wg katalogu, niestety , jest to tylko pewne przybliżenie. Do jego doświadczalnego wyznaczenia trzeba mieć odpowiednie zaplecze techniczne.

W swoim zakładzie pracy, dla tworzenia formularzy kart kontrolnych, doprowadzamy proces do stanu stabilnego i prawidłowego pod względem wymagań specyfikacji i co godzinę pobieramy 3 kolejne wypraski przez 24 godziny (72 dane pomiarowe dla 1 parametru). Pomiar masy wypraski na wadze elektronicznej  można wykonać zaraz, natomiast pomiar liniowy należy dokonać po wyrównaniu temperatury wypraski do temperatury otoczenia czyli dla grubości ścianek 2÷3mm, według naszego doświadczenia, po godzinie. Takie samo postępowanie będzie przebiegało w trakcie pracy (wypełniania) z formularzem z uwzględnieniem poprawek na liniową rozszerzalność termiczną. Należy wykonać tabelę z poprawkami dla wszystkich temperatur jakie mogą wystąpić na stanowisku technologicznym, z odniesieniem do 20°C .

Natomiast wartości odkształceń określa się po 16 godzinach, nie jest to więc w ścisłym znaczeniu SPC, ale kontrola wyrobu. Można jednak doświadczalnie interpolować zmianę odkształcenia do np. 1 godziny i w przypadku gdy jest to parametr krytyczny i wykorzystać do sterowania procesu. W firmie NYPRO pod Dublinem zastosowano karty kontrolne parametru odkształcenia  do sterowania wtryskiwania obudów dyskietek. Do stabilizacji termicznej kształtu użyto obudowanego taśmociągu odbierającego wypraski.

Dane z wzorcowego procesu są wpisywane do arkusza Excel’a,  generując w następnym arkuszu skoroszytu, formularz karty kontrolnej. Jedynie zwykle trzeba wyedytować oś x na wykresie i ją przeskalować. Na innych arkuszach skoroszytu są informacje pomocnicze: opis posługiwania się arkuszami, wykresy pomiarów wzorcowych, rozkład itp.

PRACA Z KARTAMI KONTROLNYMI

Po opracowaniu na podstawie procesu wzorcowego formularza karty kontrolnej, obsługa na stanowisku pracy zaznacza punkty pomiarów danej próby i wykreśla linie łączące punkty środkowe czyli punkty median. Przebieg wykresu świadczy o zachowaniu stanu uregulowania lub wystąpieniu zakłócenia procesu nie wynikłego z przyczyn losowych. Tylko takie przyczyny losowe wpływały na przebieg procesu w procesie wzorcowym.

Przykładowo prawdopodobieństwo, że pojedyncza mediana z badanej próbki dla karty kontrolnej będzie leżała powyżej linii centralnej wynosi 0,5. Jest to prawda, pod następującymi warunkami:

1.      proces jest uregulowany (wartość linii centralnej jest zgodna ze średnią z populacji),

2.      kolejne mediany z badanych próbek są niezależne

3.      rozkład median jest zgodny z rozkładem normalnym.

Krótko mówiąc, jeśli są spełnione powyższe warunki, to prawdopodobieństwo wystąpienia mediany z próbki powyżej lub poniżej linii centralnej wynosi 50 procent. Tak więc prawdopodobieństwo pojawienia się dwóch kolejnych median z próbki powyżej linii centralnej wynosi 0,5 razy 0,5 = 0,25.

Zgodnie z tym, prawdopodobieństwo tego, że 9 kolejnych próbek będzie się znajdowało po jednej stronie linii centralnej wynosi 0.5⁹ = 0.00195. Zauważmy, że jest to w przybliżeniu prawdopodobieństwo, przy którym pojedyncza próbka przekracza górną lub dolną linię kontrolną wyznaczoną na podstawie kryterium 3 razy sigma (przy rozkładzie normalnym i procesie uregulowanym). Dlatego można uznać 9 kolejnych próbek powyżej lub poniżej linii kontrolnej jako inny, dodatkowy sygnał o rozregulowaniu procesu. Poniżej zostaną opisane te dodatkowe sygnały.

Jak już wcześniej podano, obszar poniżej i powyżej linii centralnej jest podzielony na trzy pary domyślnych stref, są one zdefiniowane pomiędzy wartościami obliczonymi dzięki regule sigm. 2 strefy A umieszczone  są między wielkością 2s i 3s,  strefy C leżą nad i pod  linią centralną, a strefy B są pomiędzy A i C ( od 1s i do 2s ), wszystkie symetrycznie poniżej i powyżej linii centralnej.

·               9 kolejnych punktów po jednej stronie linii centralnej. Jeśli zostanie zaobserwowany taki przypadek (np. wykrył to test wzorca przebiegu), to prawdopodobnie na proces ma wpływ jakiś istotny czynnik. Jeśli 9 kolejnych obserwacji leży poniżej lub powyżej linii centralnej, to można domniemywać, że średnia procesu uległa zmianie. Zwróćmy uwagę, że monitorując proces za pomocą kart kontrolnych oczekuje się, że kolejne punkty kreślone na wykresie będą symetryczne wokół linii centralnej. W przypadku kolejnych sekwencji obserwowanej zmiennej diagnostycznej leżących po jednej stronie linii centralnej należy spodziewać się tego, że proces został zakłócony. Sygnału tego nie należy wykorzystywać przy monitorowaniu procesu za pomocą kart R, S oraz wielu kart oceniających właściwości alternatywnie. Jednakże, wtedy, gdy sygnał taki jest rejestrowany dla wyżej wymienionych kart, jego wykrycie może sugerować inżynierowi kontroli jakości ewentualne przesunięcie badanej wielkości. Na przykład, wartości kolejnych próbek dla karty kontrolnej, badającej wariancje leżące poniżej linii centralnej, mogą być cenną wskazówką o jaką wartość zmniejszyła się wariancja badanego procesu.

·               6 kolejnych obserwacji wzrasta lub maleje. Ten test wskazuje na dryf średniej procesu. Zwykle taki dryf jest skutkiem zużycia maszyn, nieodpowiedniej konserwacji, polepszenia umiejętności obsługi itp.

·               14 kolejnych obserwacji na przemian w górę i w dół. Jeśli zostanie wykryty taki sygnał, to można się spodziewać, że na proces mają systematyczny wpływ dwie przeciwstawne przyczyny. Przykładowo, monitorowane są na przemian wyroby z dwóch różnych źródeł.

·               2 z 3 kolejnych obserwacji w strefie A. Pozytywny wynik tego testu jest tak zwanym sygnałem ostrzegawczym o przesunięciu wartości badanej zmiennej. Zauważmy, że prawdopodobieństwo fałszywego sygnału o rozregulowaniu procesu (proces przebiega prawidłowo, a test wskazuje, że proces jest rozregulowany) dla tego sygnału wynosi w przybliżeniu 2 procent.

·               4 z 5 kolejnych obserwacji w strefie B. Tak jak poprzednio sygnał ten można traktować jako sygnał ostrzegawczy o przesunięciu badanej wielkości zmiennej. Również w przypadku tego testu prawdopodobieństwo fałszywego sygnału o rozregulowaniu procesu wynosi w przybliżeniu 2 procent.

·               15 kolejnych obserwacji w strefie C (powyżej lub poniżej linii centralnej). W przypadku, gdy 15 kolejnych obserwacji leży w strefie C (po obu stronach linii centralnej) można przypuszczać, że odchylenie standardowe procesu uległo zmniejszeniu. W tym przypadku jest to bardzo dobry sygnał. Bardziej ustabilizowany proces wymaga nowych granic kontrolnych i daje większe C_pk.

·               Żadna z 8 kolejnych obserwacji nie leży w strefie C. Test ten wskazuje, że na pobierane próbki oddziaływają dwa różne czynniki o dwumianowym rozkładzie. Tak może się zdarzyć, gdy na przykład,  odkładane są próbki pobierane z jednej z dwóch gniazd formy lub np. z dwóch miejsc pomiaru grubości folii. Jedno gniazdo generuje strumień wyrobu powyżej średniej, druga poniżej średniej.

·               Zasadniczy warunek uregulowania procesu to żaden punkt wykresu median nie przekracza linii kontrolnych.

Opisane wyżej zależności wynikają z teorii statystycznych ale w praktyce często trudno się w pełni do nich stosować. Tym bardziej że nawet w normie [3] można przeczytać bardzo istotną uwagę: „... żaden proces nie jest w pełni statystycznie uregulowany.”

 MODYFIKACJE KART KONTROLNYCH

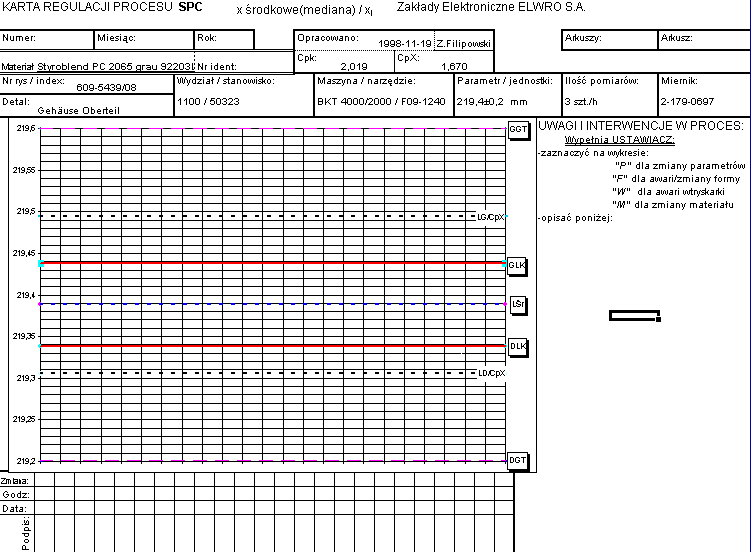
W poprzednim numerze VTS Przedstawione są klasyczne karty kontrolne przez nas stosowane: karta bez granic tolerancji (masa) oraz wymiaru liniowego z granicami tolerancji i  obliczoną wielkością C_{pk ,} w tej karcie równą ok. 2,02. Ponieważ jest to wartość większa niż wymaga w specyfikacji odbiorca wprowadziliśmy oprócz linii kontrolnych GLK, DLK, linii środkowej Lśr wynikłych z procesu wzorcowego oraz granic tolerancji GGT, DGT także dodatkowe linie kontrolne górną i dolną LG/CpX, LD/CpX, które wynikają z narzuconego specyfikacją dotrzymania wskaźnika C_pk. W przypadku naszego odbiorcy ( także zaleceń ogólnych dla dobrych wyrobów ), jest to wartość CpX=1,67. Jeżeli wykres opisujący proces będzie przebiegał między tymi liniami, to ten warunek będzie dotrzymany przy założeniu, że średnie odchylenie standardowe nie ulegnie zwiększeniu. Tak zmodyfikowana karta ( ten sam proces wzorcowy jak w 2/2000 VTS ) wygląda następująco:

 Wprowadzono także poprawkę na występujący skurcz wtórny. Należy wyznaczyć ją doświadczalnie, z dużej próbki i pod wyżej opisanymi warunkami stałej temperatury. Na formularzu poprawka modyfikuje przebieg linii LG/CpX i LD/CpX. Właśnie taką kartę stosujemy w naszej praktyce, oto ona:

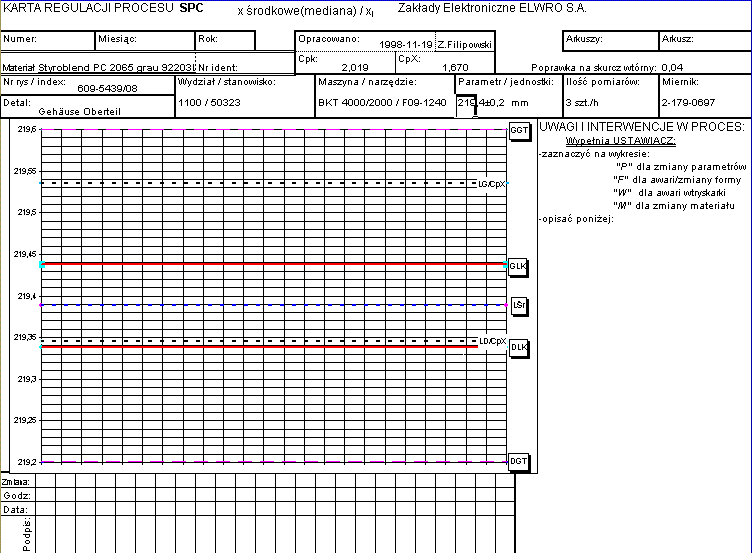
W stosunku do poprzedniej karty widzimy że tylko przekroczenie GLK (górnej) gwarantuje pewność C_pk=1,67.W poprzedniej wersji karty bez poprawek, dolna granica  DLK pozornie miała zapas który tu wykorzystany jest przez poprawkę na skurcz wtórny, nawet w niewielkim zakresie wewnątrz granic kontrolnych.

Alternatywnie zamiast tego można by przesunąć tylko granice tolerancji:   

 …GT_1h = …GT_¥ + (poprawka na skurcz wtórny)     

karta kontrolna może wtedy wyglądać tak:                   

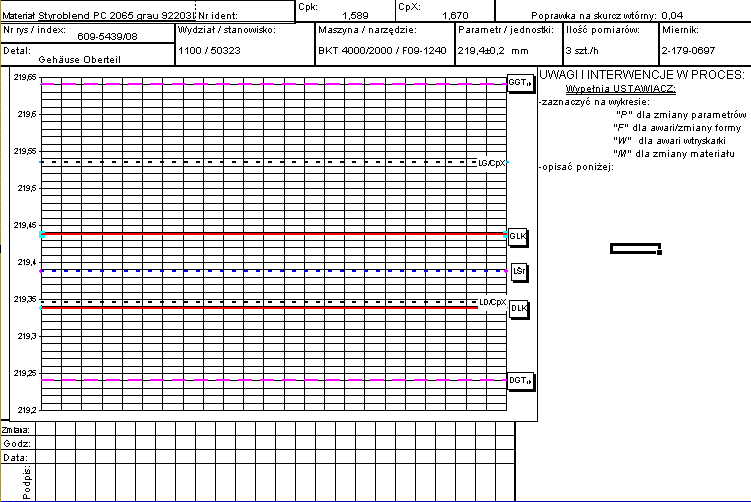
 Dalej widać że należy pracować w górnym zakresie obszaru wewnątrz granic kontrolnych lub jeszcze lepiej starać się zmienić proces na dający wyrób o większym wymiarze w zakresie 219,4±0,2 ale równie dobrym C_p.

Obie karty z poprawkami właściwie są takie same, gdyż liczą się tylko wzajemne linii środkowej i kontrolnych …LK  i ­ L…/CpX. Można by na jednym wykresie umieścić wszystkie linie z jednej i drugiej karty z poprawkami ale zaciemniło by to tylko obraz.

W tych warunkach GLK i DLK należy traktować jako wewnętrzne granice kontroli procesu (stanu uregulowanego) zgodnego z procesem wzorcowym. natomiast LG/CpX i LD/CpX, o ile leżą na zewnątrz zakresu GLK ÷ DLK,, należy traktować jako linie zewnętrzne. Jeżeli któraś z linii leży wewnątrz zakresu GLK ÷ DLK to należy starać się proces prowadzić wewnątrz zakresu …LK ÷ ­L…/CpX. Taki przypadek może wystąpić, gdy prowadzi się proces ze względu na więcej niż jeden parametr z granicami kontrolnymi.

Karty kontrolne prowadzą bezpośrednio pracownicy obsługujący wtryskarki. Od chwili wprowadzenia kart kontrolnych ręcznie wypełnianych nastąpiła aktywizacja czynnej samokontroli. Rezultatem było uzyskanie 0 ppm braków po  rocznej ocenie odbiorcy.

W następnym numerze VTS zakończymy temat SPC wnioskami ze stosowania kart kontrolnych w automatycznych modułach programów sterujących maszyn w porównaniu z wyżej przedstawionymi ręcznie prowadzonymi kartami.

Literatura

1.    a. Iwasiewicz: Statystyczna kontrola jakości w toku produkcji. Systemy i procedury.

PWN, Warszawa 1985.

2.    PN-ISO 3534-2:  Statystyka. Statystyczne sterowanie jakością. Terminologia i symbole

3.    PN-ISO 8258 + AC1: Karty kontrolne Shewharta.

4.    H. Helmers: SPC - Statystyczne sterowanie procesem. Praktyczne Sterowanie Jakością. Alfa Weka 1997.

5.    H. Helmers, R. Stark: SPC in der Continental. Qualität und Zuverlassigkeit 1988, 33, 2, 71-75.

6.    Program: Demo STATISTICA for Windows 5.1.  Statsoft. Inc.

Z. Filipowski: SPC – Statystyczne sterowanie procesem wtryskiwania tworzyw sztucznych. Postęp w przetwórstwie tworzyw sztucznych. Politechnika Częstochowska 1997, s.237-243

Zdzisław Filipowski

 Wróć na górę